So, in my first post about the beat tracking, I decided that I would use a tap tempo button to set the frequency of wiper action. This would involve me hitting a button along to the beat of the song to program in the beat.
Over the weekend, one of my friends convinced me that that was too easy, and this project would only be cool if it was automatic. So I guess I’m making it automatic…
Concept
The goal of software beat tracking is to calculate the “energy” of a song at various beats per minute (BPM) and decide based on that which beat has the highest energy. What I mean by “energy” is the “amount of sound”. Basically, you want to find the tempo at which the most stuff happens.
There are a number of ways to do this, but I need one that will not be very processor intensive so that my little AVR can handle it. I found a method online and tried it out using a python script achieving pretty good results.
Pre-filtering
To take the load off the AVR, I will be implementing quite a bit of filtering in hardware to condition the sound waveform into a form I can use. In the case of this Python script though, I needed to write some code and do some other digital processing to do that filtering for me.
LPF
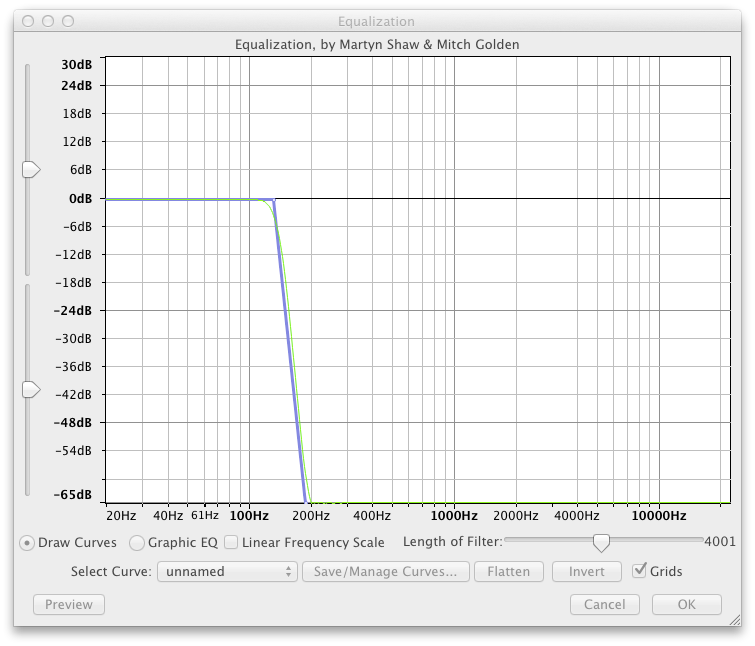
A lot of songs with really steady beats tend to have them in the lower frequencies (bass, kick drum, etc), so I started by importing my song (Propane Nightmares) into Audacity and applying a sharp Low Pass Filter using the “Equalization” effect with a cut off at around 160Hz:
Into this:
Now, I know that I’m not going to get that sharp of a filter with the simple one-pole filters I used on the glasses and jacket, so I’ll be looking at some new topologies to get a tighter cutoff. Even still, the filter I used here is pretty generous, but …meh.
Envelope
Sound familiar? Just like in the glasses and jacket, I needed a waveform of the general “loudness” to get an idea of what was a beat and what was just noise. Again, this will all be done in hardware on the actual device, but for now, I did it in Python.
I started by deleting one of the channels of the song in Audacity and exporting it as a mono 16 bit .wav file. This file was easily imported into Python using the wave package. This package lets you import .wav files and read the actual audio data samples frame by frame. In my case, I had 44100 samples per second.
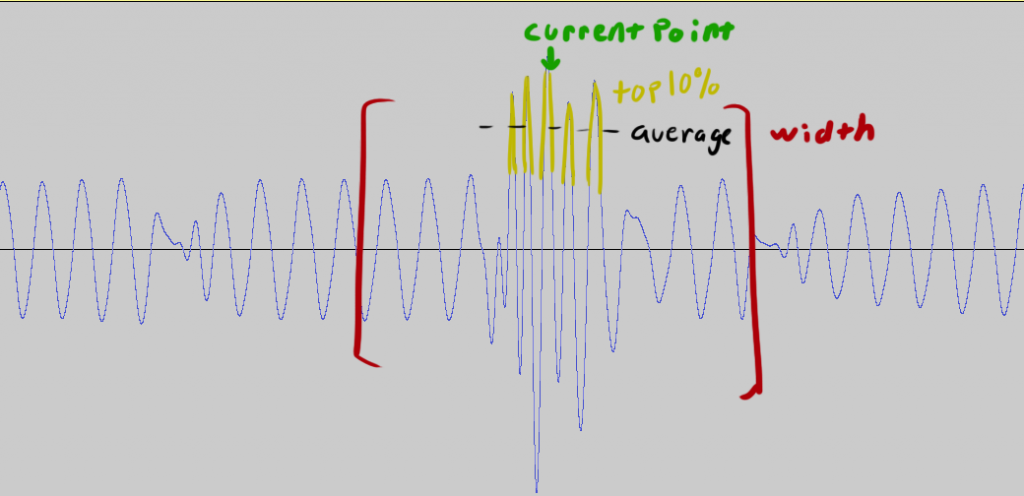
To calculate the value of the envelope at any given point, I created a function that takes a song file, a position in that song file (in samples, not seconds), and the desired envelope size and returns the average of the top 10% of samples residing within one envelope’s distance of the current point. Note that the “top 10%” were ordered by number, not magnitude (distance from zero). In this way, my envelope should always be positive assuming my envelope is wide enough (i.e. all the negative samples in the envelope are in the bottom 80%). Here’s a graphic to explain:
Here’s the function:
def rollingenvelope(song,position,width):
if (position<song.getnframes()):
envelopebuffer = []
start = 0 if position-width<0 else (position-width) #handle the case where the envelope under runs the beginning of the file
end = song.getnfranes() if position+width > song.getnframes() else (position+width) #handle the case where the envelope overruns the end of the file
for i in range(start,end):
song.setpos(i)
envelopebuffer.append(struct.unpack_from('h',song.readframes(1))[0])#grabs the decimal value of the current frame
return numpy.average(sorted(envelopebuffer)[-(width/10):])
else:
print 'Position out of range'
return 0
Plotting these average values along the timeline of the audio waveform gives you the envelope as you can see here:
By the way, this plot was made using matplotlib which I highly recommend.
Differentiator
The best next step would be to pass the envelope waveform through a differentiator which would create sharp positive spikes whenever the envelope rises sharply (at the onset of a beat) and sharp negative spikes when the envelope falls sharply (at the end of a beat). Passing this through a half-wave rectifier would make all of the spikes positive. I didn’t do this step because it would have been too much of a pain to implement in software. I imagine any way to focus down each beat to a single point in time will aid in precisely measuring the beats though, so I’ll be trying it in hardware when I get there.
Comb Filter
Now that all of that pre-filtering is done, it’s time to implement a comb filter and actually measure the bpm. A comb filter is a form of convolution that simply convolves the input signal with an impulse train. I applied a comb filter to the sample with the comb set at various BPM and plotted the results. The idea is that the comb that most closely matches the BPM of the actual song will return the highest value and show up on the graph as a peak.
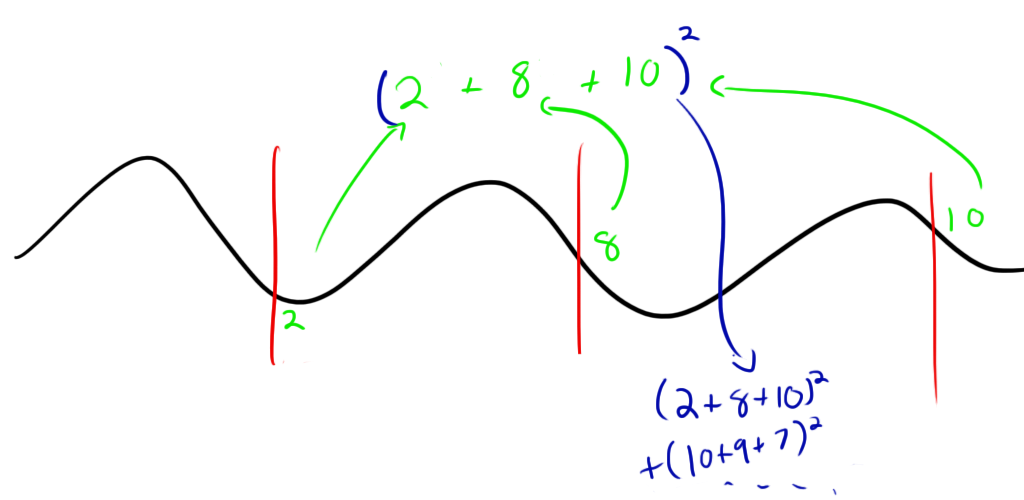
If you don’t know what convolution is (don’t worry, I don’t either) or otherwise have no idea what I’m talking about, here’s a graphical example: First, you take your waveform: 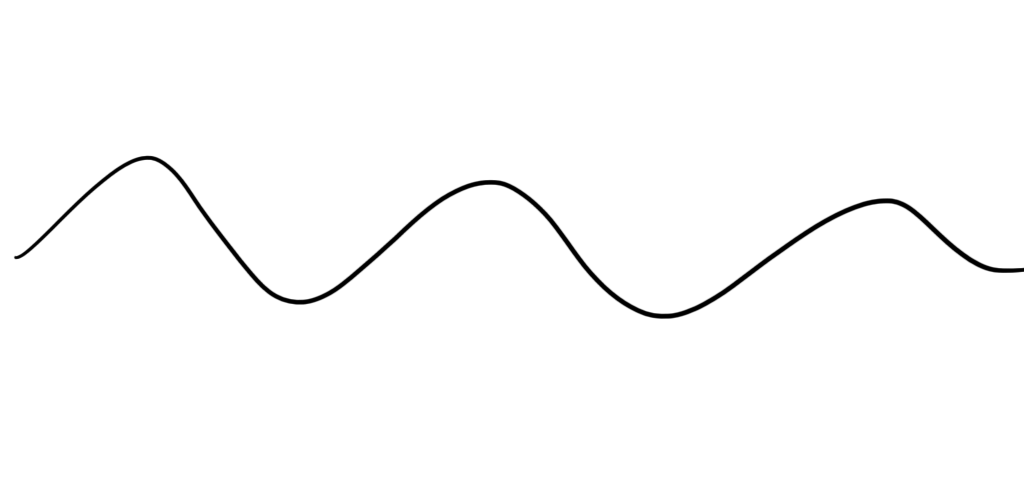 Then you overlay on top of it a “comb” of “teeth” at evenly spaced intervals. In my code, I used a comb with three teeth. Each of the teeth had a value of one. The teeth should be spaced out by the appropriate amount of time to represent the BPM in question. i.e. a 60 BPM comb would have teeth spaced by 1 second.
Then you overlay on top of it a “comb” of “teeth” at evenly spaced intervals. In my code, I used a comb with three teeth. Each of the teeth had a value of one. The teeth should be spaced out by the appropriate amount of time to represent the BPM in question. i.e. a 60 BPM comb would have teeth spaced by 1 second. 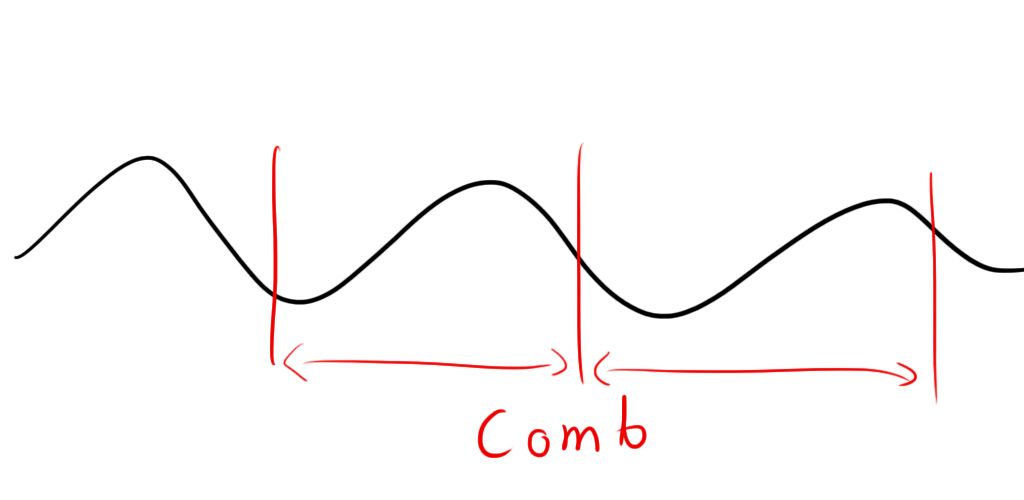 At each point in the comb, you multiply the tooth’s value (1 in this case) by the value of the waveform it’s sitting on and sum those three together.
At each point in the comb, you multiply the tooth’s value (1 in this case) by the value of the waveform it’s sitting on and sum those three together. 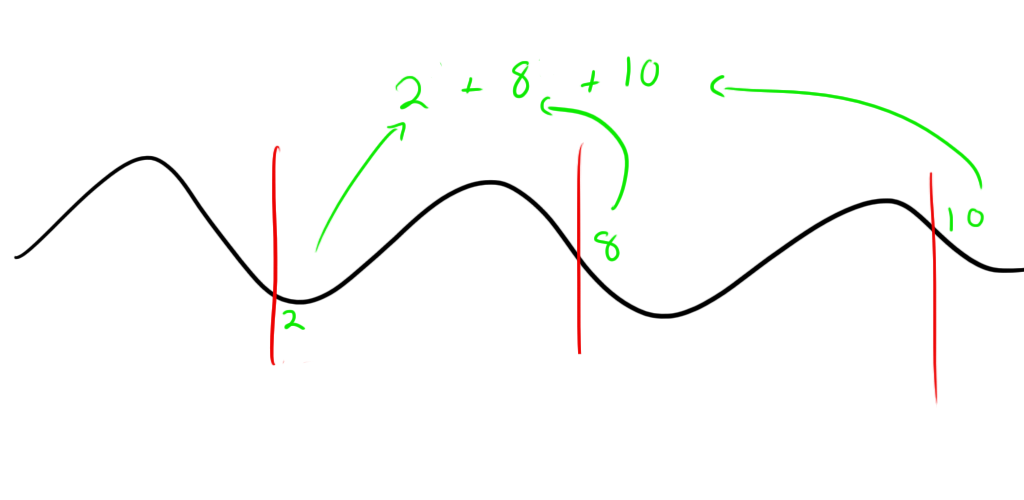 You then move the comb a small amount in the waveform and do it again:
You then move the comb a small amount in the waveform and do it again: 
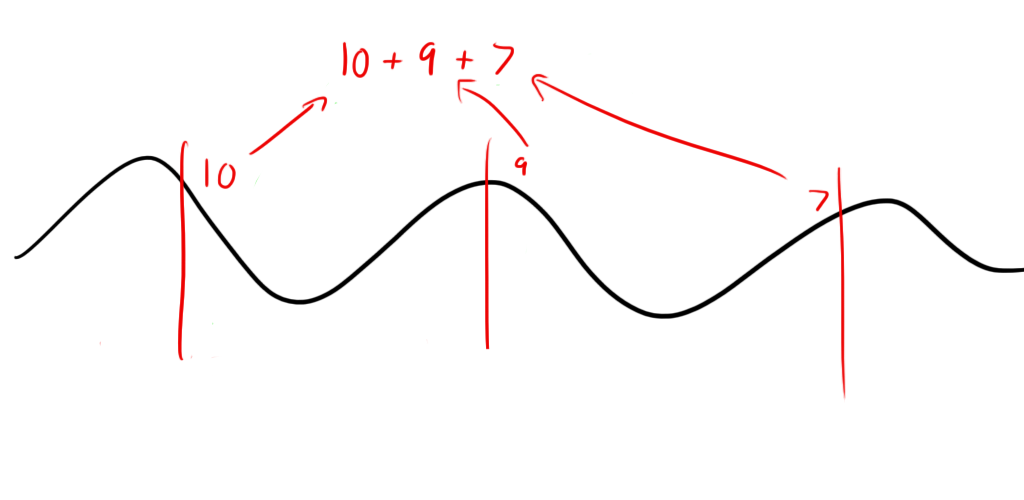 This example has the teeth lining up pretty well (but not perfectly) with the waveform so the value is pretty high. Now you want to add all of these up and keep shifting and adding until some designated stopping point. In my code, I picked just a 3-4 second sample out of the middle of the song and did my comb along that sample. The numbers might be a little more manageable if you divide the sum by the number of samples and take an average though it’s not necessary.
This example has the teeth lining up pretty well (but not perfectly) with the waveform so the value is pretty high. Now you want to add all of these up and keep shifting and adding until some designated stopping point. In my code, I picked just a 3-4 second sample out of the middle of the song and did my comb along that sample. The numbers might be a little more manageable if you divide the sum by the number of samples and take an average though it’s not necessary.
Now, if you actually try this, you’ll notice that it doesn’t work. This is because simply adding the three points together like this will yield the same results at any comb BPM. You can think of it as doing each of the three teeth independently. As long as all three start and stop at approximately the same point in the sample, at different BPM spacing, they will all produce roughly the same values regardless of BPM. 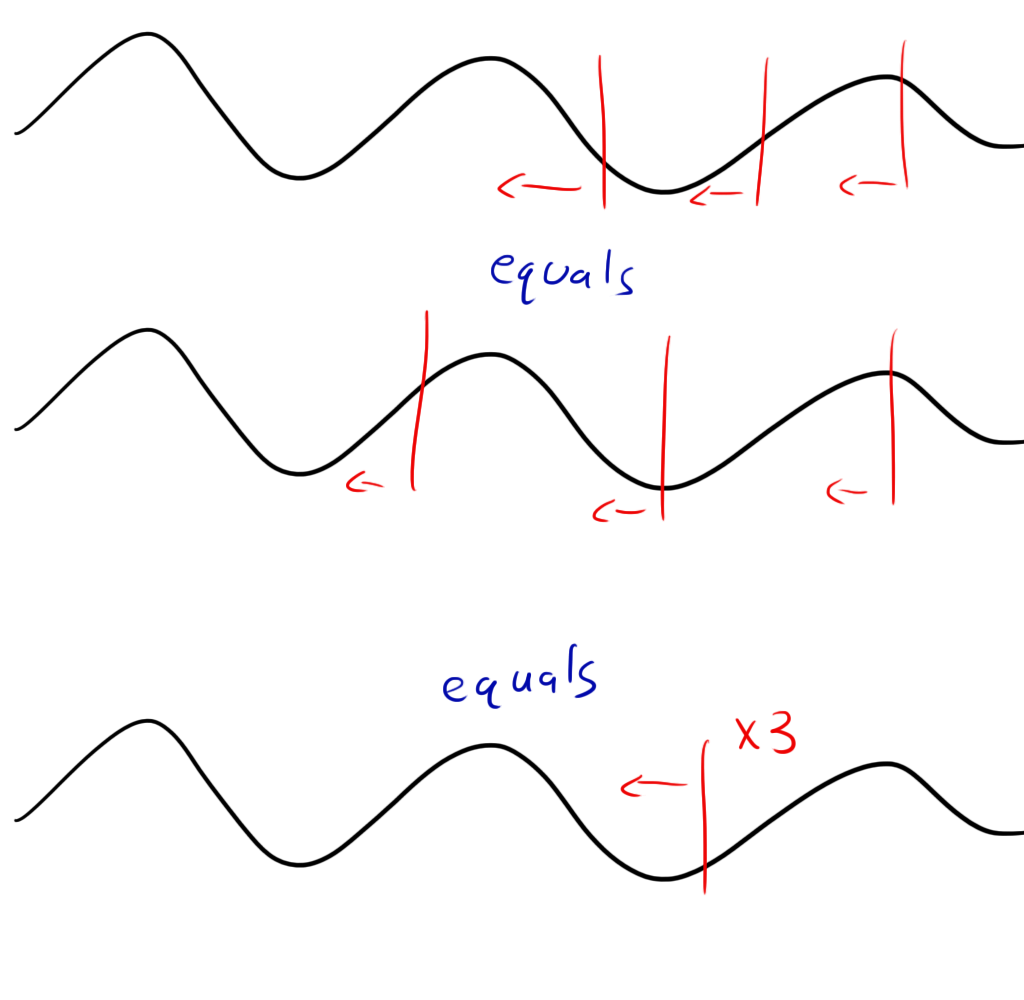 What you need to do is calculate how well the comb does with its teeth specifically spaced that far apart. Essentially, you want to make sure that when the teeth line up with the waveform exceptionally well, they produce a very large value. One way to do this is to square each sum before adding it to the rest. If they line up moderately well, you’ll get a moderate answer, but if they add up very well, you’ll get a very large answer.
What you need to do is calculate how well the comb does with its teeth specifically spaced that far apart. Essentially, you want to make sure that when the teeth line up with the waveform exceptionally well, they produce a very large value. One way to do this is to square each sum before adding it to the rest. If they line up moderately well, you’ll get a moderate answer, but if they add up very well, you’ll get a very large answer.
What’s actually happening here is that we’re using a method invented by Mr. Gauss:
Fuck yeah Carl!
It’s called “Least Squares“. Least squares is a method for finding a function that best fits a set of data. Here, we’re trying to find a function (in this case, a comb) that fits our data (matches its BPM). Normally with least squares, you would calculate your error (how far off you were) at each step and square it. The guess with the least squared error when summed over all data points is the closest guess you’re going to find.
For our function, we’re sort of doing the opposite. Instead of calculating error, we’re calculating success, so instead of looking for a minimum, we’re looking for a maximum.
Here’s my comb filter function. It takes the envelope and the BPM being guessed and returns a value proportional to how closely the BPM matches the song.
def trybeat(envelope,bpm):
energy = 0
gap = int(bpm2numsamples(bpm)) #converts BPM to samples per beat
if (len(envelope)<=2*gap): #envelope waveform is too small to fit the comb.
return 0
else:
for i in range(0,len(envelope)-(2*gap)):
energy += (envelope[i]+envelope[i+gap]+envelope[i+2*gap])**2
energy = energy/(len(envelope)-(2*gap)) #take the average so that the function doesn't favor smaller combs that can calculate more values before the hit the end of the envelope waveform
return energy
Results
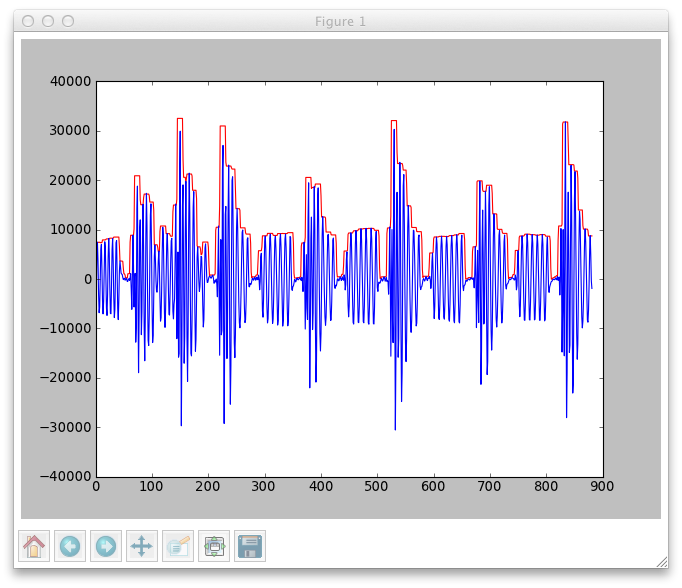
After running the comb filter on a number of BPMs, I plotted the results. Here are the results for the song “Propane Nightmares” On the x axis is BPM. Don’t worry about the units on the y axis, just know that they are proportional to “loudness”.
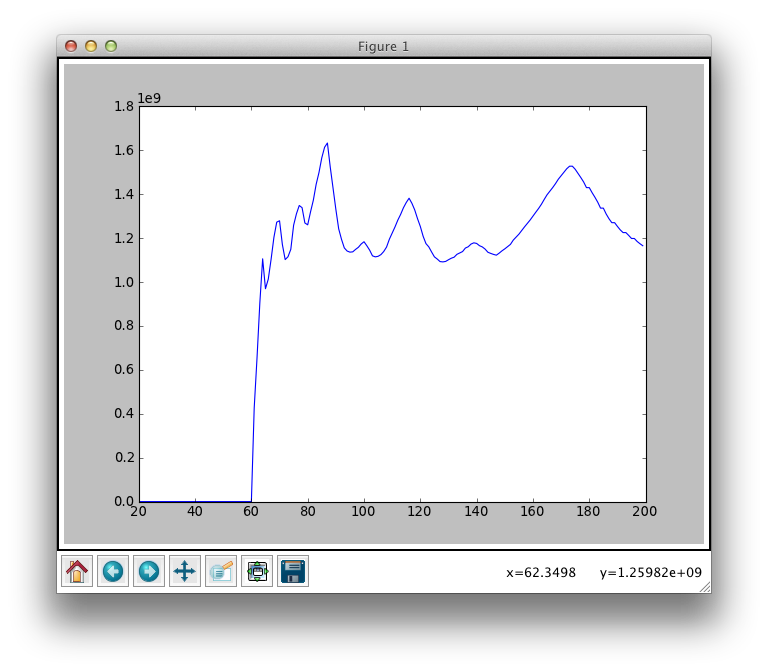
You’ll note the gradual peak that is centered at around 175 BPM and a huge harmonic at 87 (half of the actual BPM). 175 is the correct BPM for the song. Here’s the song and an online metronome so you can try it yourself (note that I took my measurements from the center of the song, so you might want to start there). The drop off on the left is due to the fact that there wasn’t enough time in my sample to even fit the comb filter even before shifting it, so the function returned zero.
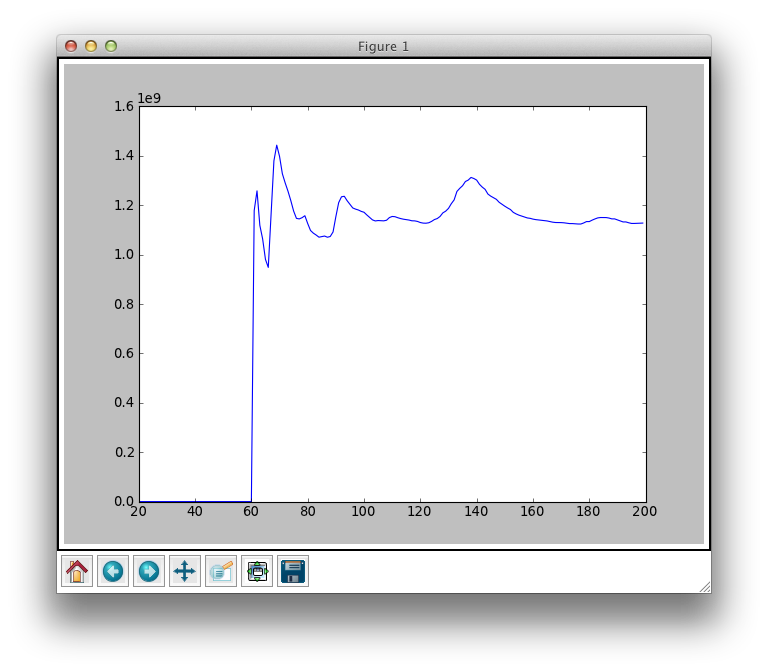
I also tried it with some other songs. Here’s Broken Boy Soldier by the Raconteurs.
With BPM around 139 with a rather large harmonic at 68 BPM.
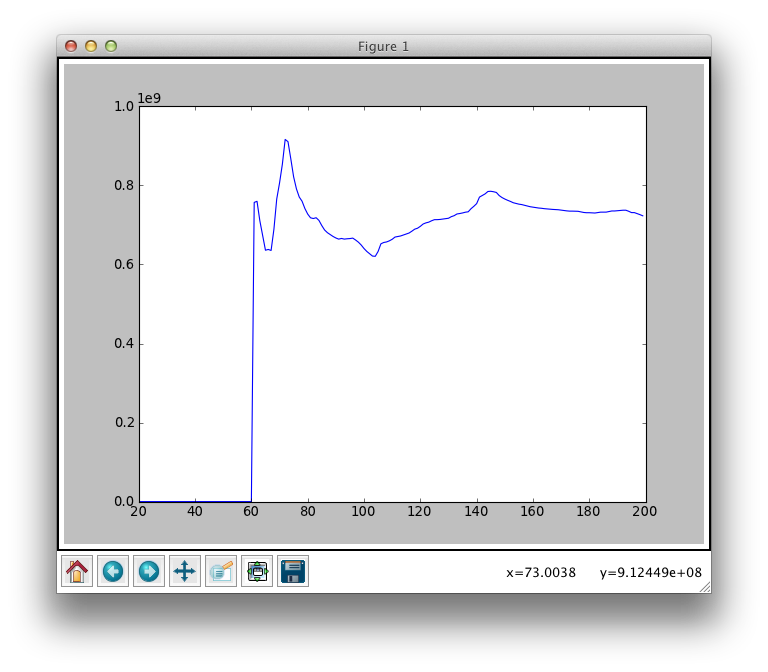
And Call It a Day also by the Raconteurs:
With BPM around 73. I was surprised this one turned out so well considering that it’s not exactly dance music with a strong beat.
Conclusion
Now, these calculations aren’t exactly cheap from a processing standpoint. I had to run a comb filter on almost 200 different frequencies which takes a lot of time. What I did find that was interesting is that a lot of times, the correct BPM has a ramp up to it, so I might be able to save some time using a sort of genetic algorithm that will make some intelligent guesses as to where the peaks are based on the slope of its current guess.
I was also surprised how strong the harmonics are. I suppose a lot of times, my code would incorrectly identify half the BPM as the actual BPM. This isn’t the end of the world though; for a lot of the faster songs, the wipers won’t be able to keep up with the actual BPM anyway, and they will definitely appear to be intelligently keeping the beat even at half the BPM.
One other way to improve my results is to do the same method with the treble beats in addition to the bass beats. An ideal beat tracker would take a Fast Fourier Transform (FFT) of the song at various frequencies, do the comb filters for each frequency band and pick the beat that fits the best with the largest number of frequency bands.
This would be insanely processor intensive, but I could probably filter a few bands with some good analog band pass filters to take the load off the AVR. It might not be necessary, but I’ll keep my options open.
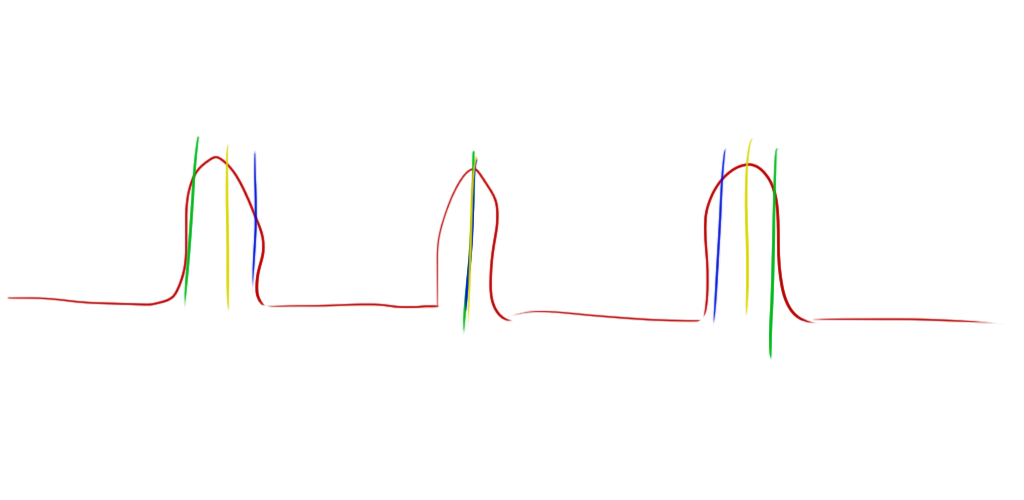
The width of the peaks in some of my graphs is inconvenient because having a very round peak makes it hard to pick an absolute correct BPM. The roundness of this BPM peaks is due to the width of the beats in the envelope. If you recall the envelope image above:
The red envelope waveform has some pretty wide peaks. This can cause combs at different BPM to return similar results. As you can see in this image, all three of these combs (yellow, green, blue) return almost the same value though they differ quite a bit in BPM:
There are two solutions to this problem.
- I could make the comb larger. More teeth makes the margin for error much smaller. This solution will require more processing power from my AVR, so I’ll have to see how many teeth I can get away with.
- I could include the differentiator which I was planning on using anyway. This would turn the wide envelope pulses into very slim pulses that only appear at the onset and end of the beat.
So, I call this experiment a success and now just have to figure out how to fit the algorithm on to a 8 bit micro controller with 1k of ram!
Continue this story here.




Couldn’t you find ready-made code?
The point here is to figure out how to do it myself. Besides, there probably isn’t any beat-tracking code for micro-controllers anyway.