In my last post, I attempted to reverse engineer an EL wire power supply to see how it worked. This brought up a few more questions that I decided to investigate, and the following investigation brought me to the brink of insanity and back. I started to doubt the very consistency of space and time as time and time again my measurements seemed to prove what I knew should be impossible.
Seriously, ask any of my friends. I haven’t been able to shut up about this all week.
Disclaimer
What follows is a very math/physics intensive and very dry explanation of some of the unique properties of inductors and transformers. I originally intended to try to spice things up by making this post into a video “chalk-talk” where I could talk through my math, but after numerous attempts, I have realized that I do not have a concrete enough understanding of these topics to put myself on the spot like that. Hopefully this post will suffice.
If you find any mistakes in my work, please let me know! I’ll be sure to update it.
A Terrible Discovery
The morning after publishing my EL wire post, I decided it would be fun to check my work. In the post, I determined the turns ratio of the supply’s transformer by measuring the inductances of each winding and taking
![]()
to get the turns ratio. I came up with approximately 1:22.
This seemed to make sense because the input/output voltage ratio was approximately 1:22 as well (5V-ish in, 100V-ish out). Well, I set to work disassembling one of my transformers to count the windings:
 There was a layer of protective tape around the wires and of course the inductor core itself. The core was comprised of two E-shaped pieces that were glued together. Unfortunately, I was unable to get to the wire without breaking the core apart. The primary winding came off easily:
There was a layer of protective tape around the wires and of course the inductor core itself. The core was comprised of two E-shaped pieces that were glued together. Unfortunately, I was unable to get to the wire without breaking the core apart. The primary winding came off easily:
 I counted about 30-35 windings on each of the two taps. The secondary winding wasn’t as easy to unwind. It was made from extremely thin wire that broke about 15 turns in. At this point, I was unable to find the end of the wire (like when you lose the end of the scotch tape), and decided to take a different approach:
I counted about 30-35 windings on each of the two taps. The secondary winding wasn’t as easy to unwind. It was made from extremely thin wire that broke about 15 turns in. At this point, I was unable to find the end of the wire (like when you lose the end of the scotch tape), and decided to take a different approach:
 Nothing a dremel couldn’t fix.
Nothing a dremel couldn’t fix.
Now all I had to do is count how many bits of wire there were. Sure, it’s a little tedious, but I only expected there to be 600-800 (22×30) of them, so it couldn’t be too bad.
So I started counting, and got a little concerned when I reached 700 and didn’t seem to be even close to done. When I got to 1000, I knew something was wrong.
 Okay, so this sucks. Clearly my ratio is much higher than 1:22. How high is it?
Okay, so this sucks. Clearly my ratio is much higher than 1:22. How high is it?
Bringing in the Big Guns
I needed a better method of measuring inductance. For this, I turned to an Agilent LCR meter that I borrowed (they usually run around
![Rendered by QuickLaTeX.com 400). Here's what it came up with for the secondary winding. <a href="http://ch00ftech.com/wp-content/uploads/2012/04/IMG_8977.jpg"><img class="aligncenter size-full wp-image-1461" title="IMG_8977" src="http://ch00ftech.com/wp-content/uploads/2012/04/IMG_8977.jpg" alt="" width="1024" height="683" /></a> 414 mH is not that far away from the 450mH I estimated in the last post. Not too bad. Now for the primary winding: <a href="http://ch00ftech.com/wp-content/uploads/2012/04/IMG_8976.jpg"><img class="aligncenter size-full wp-image-1462" title="IMG_8976" src="http://ch00ftech.com/wp-content/uploads/2012/04/IMG_8976.jpg" alt="" width="1024" height="683" /></a> 98 <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-bee17ce5c29d6fa9fa02b47a477d5c06_l3.png" height="12" width="11" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\mu\]" title="Rendered by QuickLaTeX.com"/>H, that's not too ba-wait. I got <strong>900</strong><span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-bee17ce5c29d6fa9fa02b47a477d5c06_l3.png" height="12" width="11" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\mu\]" title="Rendered by QuickLaTeX.com"/>H last time! This thing is measuring an order of magnitude lower! At first, I thought I had maybe made a math error seeing how close I was to being exactly an order of magnitude off. Further examination and re-checking of measurements revealed that my math was sound, so something else had to be wrong. In the short term, this cleared some things up. Assuming the LCR meter was correct (and it was), my turns ratio is actually <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-0effdcbf12846442a48d03d1e585ab3e_l3.png" height="45" width="74" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\frac{\sqrt{414mH}}{\sqrt{98\mu H}}\]" title="Rendered by QuickLaTeX.com"/> which works out to 1:64. This means that because my primary winding was 30 turns, my secondary was 1920! That seems so much closer to the right number. <h1>So What Did I Do Wrong?</h1> The particularly strange thing is that I was able to find the same erroneous number through two different methods. This leads me to two main questions: <ul> <li>If the inductance of the primary coil is actually 1/10 what I measured, how did I repeatedly get the same (wrong) value using my measurement method?</li> <li>If the turns ratio is actually much higher, why don't I get a higher voltage at the output?</li> </ul> <h1>Parasites</h1> So, let's review my method for determining the inductance of the primary winding. When a capacitor and inductor are placed in parallel, they set up an LC oscillator. If the oscillator is excited, current will begin to flow back and forth. Essentially, energy is moved from the inductor to the capacitor and back again. When the capacitor is fully charged (maximum energy) there is no current flow (minimum energy in the inductor) and vice versa. The important thing for me is that the frequency of this oscillation is based on this formula: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-bb368c4634743bc38dbfea04fe51c9b0_l3.png" height="40" width="123" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\Large F= \frac{1}{2\pi \sqrt{L\times C}}\]" title="Rendered by QuickLaTeX.com"/> The <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-28b2576eec035d1eef34ef04b2856908_l3.png" height="12" width="14" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[F\]" title="Rendered by QuickLaTeX.com"/> is the resonant frequency, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-c1cffd8178b3dacbd503b90c0827eb9b_l3.png" height="12" width="14" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[C\]" title="Rendered by QuickLaTeX.com"/> is the value of the capacitor I placed in parallel, and <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-5adf3ba05c04888bd0bc7dd41f00f3bb_l3.png" height="12" width="12" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[L\]" title="Rendered by QuickLaTeX.com"/> is the inductance which I'm trying to find. Here's a doodle of my oscillator: <a href="http://ch00ftech.com/wp-content/uploads/2012/04/LC-osc.png"><img class="aligncenter size-full wp-image-1465" title="LC-osc" src="http://ch00ftech.com/wp-content/uploads/2012/04/LC-osc.png" alt="" width="1024" height="1024" /></a> There's just one thing wrong with this particular doodle. It shows my inductor as an ideal inductor. This is far from true. Inductors usually have some level of <em>parasitic</em> capacitance. This is a result of having a bunch of insulated copper wound up into a small space, and it's a sometimes undesired effect that isn't easily avoided. Though my inductor is not an ideal inductor, I can <em>model</em> it as one as long as I throw a parallel parasitic capacitance along with it. <a href="http://ch00ftech.com/wp-content/uploads/2012/04/LC-osc-parasitic.png"><img class="aligncenter size-full wp-image-1466" title="LC-osc-parasitic" src="http://ch00ftech.com/wp-content/uploads/2012/04/LC-osc-parasitic.png" alt="" width="1024" height="1024" /></a>Because these capacitances are in parallel, I can simply add them. So now my equation becomes. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-3288cc799dc5d3ab1911a3deb4315109_l3.png" height="44" width="185" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\Large F= \frac{1}{2\pi \sqrt{L\times (C+C_{P})}}\]" title="Rendered by QuickLaTeX.com"/> With this in mind, I ran the experiment again a few times. I also cheated a bit. Since I already knew what the inductance was, I instead solved for <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-56b22771a0f9252ab71eed79b589755e_l3.png" height="14" width="24" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[C_{P}\]" title="Rendered by QuickLaTeX.com"/>. If I didn't know the inductance, I could have found <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-56b22771a0f9252ab71eed79b589755e_l3.png" height="14" width="24" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[C_{P}\]" title="Rendered by QuickLaTeX.com"/> and <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-5adf3ba05c04888bd0bc7dd41f00f3bb_l3.png" height="12" width="12" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[L\]" title="Rendered by QuickLaTeX.com"/> at the same time using a system of equations and two data points. Here are my results: <table> <tbody> <tr> <td>Added Capacitance</td> <td>Resonant Frequency</td> <td>Parasitic Capacitance</td> </tr> <tr> <td>1nF</td> <td>41.11kHz</td> <td>156nF</td> </tr> <tr> <td>100nF</td> <td>31.83kHz</td> <td>163nF</td> </tr> <tr> <td>.22nF</td> <td>42kHz</td> <td>151nF</td> </tr> </tbody> </table> So after running the experiment three times at three different capacitor values, I got similar results for parasitic capacitance. That's reassuring. My inductance appeared to be higher because I was making the poor assumption that the capacitance was lower (i.e. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-a78a27854f9ba40256148117d158773d_l3.png" height="14" width="56" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[C_{P} = 0\]" title="Rendered by QuickLaTeX.com"/>): <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-03c290bc9bd36502069f9eab70f967c0_l3.png" height="44" width="346" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\Large \frac{1}{2\pi \sqrt{L\times (C+C_{P})}} \approx \frac{1}{2\pi \sqrt{(L+L_{error})\times C)}}\]" title="Rendered by QuickLaTeX.com"/> So if you're not careful, the same resonant frequency can get you different values for <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-5adf3ba05c04888bd0bc7dd41f00f3bb_l3.png" height="12" width="12" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[L\]" title="Rendered by QuickLaTeX.com"/>. Another cool note is that if you know the inductance (by reading it off a data sheet or something), you can quickly determine the parasitic capacitance by setting up your LC with no C at all! The parasitic capacitance can be enough to get your inductor to <em>self-resonate.</em> <em></em>It's also worth noting that my original measurement for the secondary winding wasn't nearly as far off because the parasitic capacitance on the secondary winding was much smaller (I measured about 1.9nF) So why didn't this capacitance effect the LCR meter? Well, because it was](https://ch00ftech.com/wp-content/ql-cache/quicklatex.com-28929799ad18ebeefa0c4f41021cd981_l3.png)
400 obviously.
Set Phasors to Stun
So, having this solution gave me temporary respite, but it still couldn’t help to explain why my input/output voltage ratio was wrong. Typically, voltage ratios are determined as follows:
![]()
So, how can it be that my output voltage wasn’t 64 times my input voltage? Again, I was assuming that my components were acting ideally. To solve this problem, I had to do a major refresher course of just about everything I learned in school. Looking for a solution, I came across my notes for an old power electronics lab class I took. As it turns out, Lecture 13 was on this very topic, and I still had the handout from that lecture!
 Protip: Never throw anything away ever.
Protip: Never throw anything away ever.
What follows is my attempt to work through the explanation offered in the notes.
Stick to Your Ideals
Let’s first consider an ideal transformer:
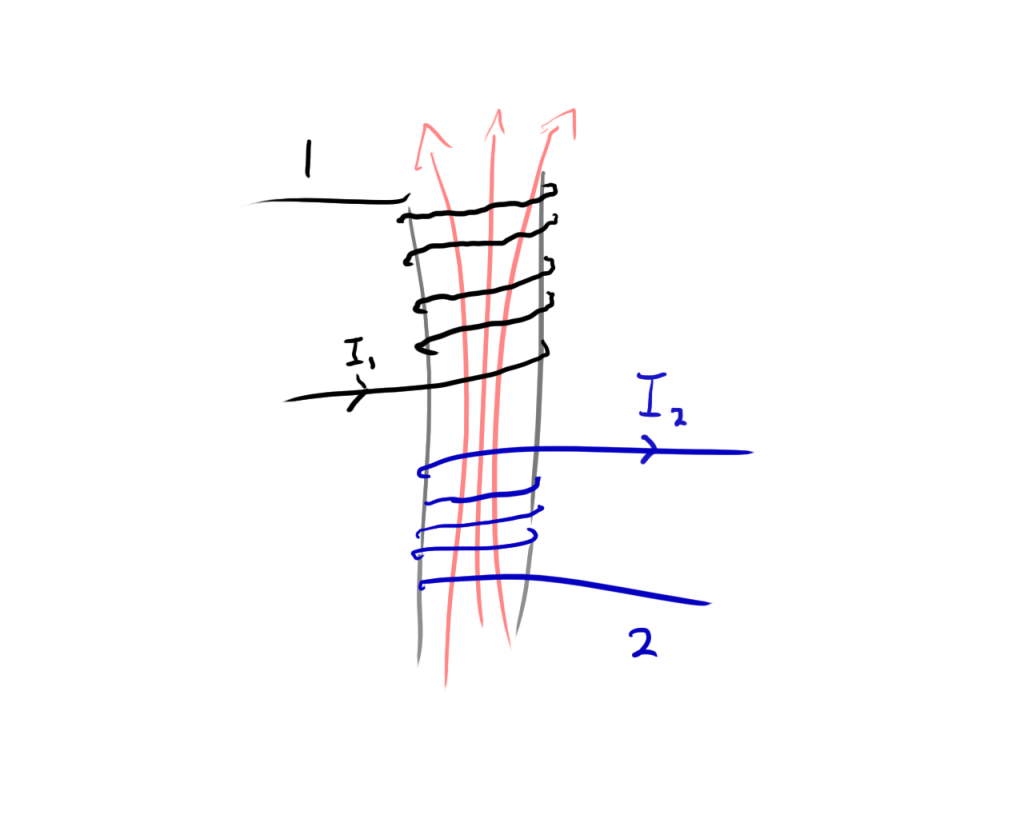 An ideal transformer is one where all of the magnetic fields generated by one winding pass through the other winding. In reality, magnetic fields will tend to fray out and pass through gaps in the windings. We can reduce this effect by using special materials in our transformer cores that are said to have a low “Reluctance”.
An ideal transformer is one where all of the magnetic fields generated by one winding pass through the other winding. In reality, magnetic fields will tend to fray out and pass through gaps in the windings. We can reduce this effect by using special materials in our transformer cores that are said to have a low “Reluctance”.
Similar to electricity traveling in the path of least resistance, magnetic fields will travel along the path of least reluctance. So these magnetic cores keep the magnetic fields in line. The total magnetic field passing through a coil is called the Magnetic Flux and is signified with a capital phi (
![]()
). This is basically, the magnetic flux density multiplied by the cross sectional area.
![]()
Makes sense. A density times an area gives you a quantity. The flux passing through a coil (or rate of change of that flux) will determine things like the voltage across the coil, so it’s generally good to know.
Keep in mind though that a piece of wire doesn’t really know anything about the geometry of the magnetic field. It only cares about how much magnetic flux is passing through the overall loop. It can’t tell if it is wrapped many times around the same small area or once around a much larger area:
 So, we usually don’t deal with flux for transformers. We instead work with “flux linkage”. Flux linkage (
So, we usually don’t deal with flux for transformers. We instead work with “flux linkage”. Flux linkage (
![]()
) is simply the magnetic flux through the core multiplied by the number of windings in the inductor:
![]()
For a single winding inductor,
![]()
. It also happens that the flux linkage for a component is equal to the time integral of the voltage across it:
![]()
So, if we know that all of the flux in one winding of the transformer also passes through the other winding (ideal, remember?) we get:
![]()
![]()
![]()
What Makes You So Perfect?
So what exactly gets a transformer closer to an ideal transformer? Lets first model our transformer as a magnetic circuit. Just like you can model electric circuits with resistors and voltage sources, you can model magnetic circuits with coils and reluctances.
So what do I mean by magnetic “circuit”? Well, you’ve probably been wondering why it seems that transformer and inductor cores always seem to form loops such as in this torroidal inductor:
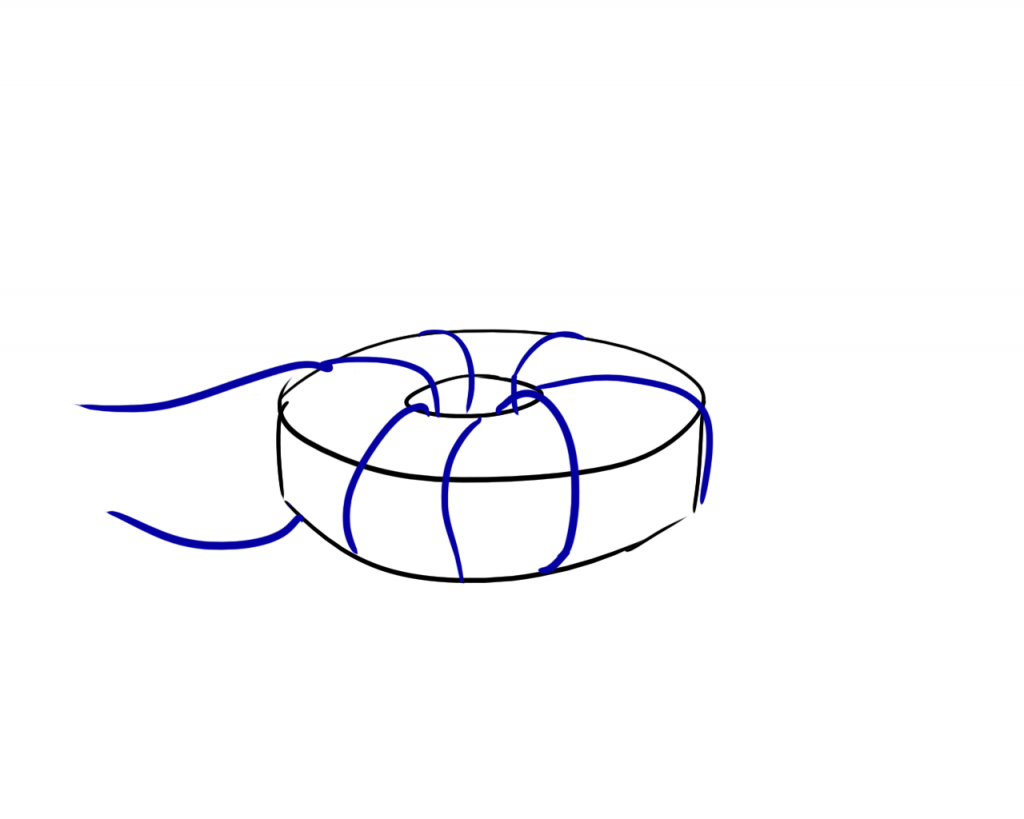 Or even in the E shaped core of the EL wire transformer:
Or even in the E shaped core of the EL wire transformer:
 Where there are actually two loops around the outside of the wire coil. This isn’t always the case though. There are a number of bar-core inductors that do not produce a loop. In this case, the bar starts the loop, but the loop is completed by the space surrounding it. Surely you’ve seen one of these:
Where there are actually two loops around the outside of the wire coil. This isn’t always the case though. There are a number of bar-core inductors that do not produce a loop. In this case, the bar starts the loop, but the loop is completed by the space surrounding it. Surely you’ve seen one of these:
 Where magnetic fields travel through air just fine. As you will see though, this is far from ideal and will create a poor transformer.
Where magnetic fields travel through air just fine. As you will see though, this is far from ideal and will create a poor transformer.
So remember how magnetic reluctance (
![]()
) is sort of like electrical resistance? Like resistance, it’s a property of the material that is creating the circuit loop. In this case, it’s a property of the core of my inductor or transformer. The lower the reluctance, the more easily magnetic fields form inside the material.
In the case of an non-looping core, you would take the reluctance of the core along with the reluctance of the air completing the loop and sum them just like summing resistors in series. In fact, even in the looping inductor core, it’s safe to say that not all of the magnetic fields pass entirely around the loop inside the core. Some of them will leak out. This is similar to having two resistors in parallel. The core will represent a low-reluctance, and the air surrounding will represent a larger reluctance. Most of the flux will pass through the lower reluctance path, but not all of it.
The formula for reluctance is:
![]()
Where
![]()
and
![]()
are the length and cross sectional area of the magnetic path, and
![]()
is the permeability of the material. I’ll go into more detail on permeability later.
The only distinction to keep in mind between reluctance and resistance is that magnetic reluctance is non-dissipative. I.e. unlike a resistor, it will not cause energy loss but will instead store energy. Not a super important point for this discussion, but something to keep in mind.
Analogous to voltage which is the “Electro-Motive Force” we have the “Magneto-Motive Force” (Yes, I know, it sounds really corny). The MMF (or
![]()
) is measured in Ampere-turns and as its name suggests is equivalent to:
![]()
Where
![]()
is the number of turns and
![]()
is the current.
So, to tie up our analogy, we need something magnetic that acts like current. Well if current is the measure of electrons passing through a cross sectional area, we can use flux because it’s a measure of magnetic fields passing through a cross-sectional area. The flux through a wire coil is given by:
![]()
Or more specifically:
![]()
Where
![]()
is the magnetic path length. So now we can draw a circuit representation of our inductor:
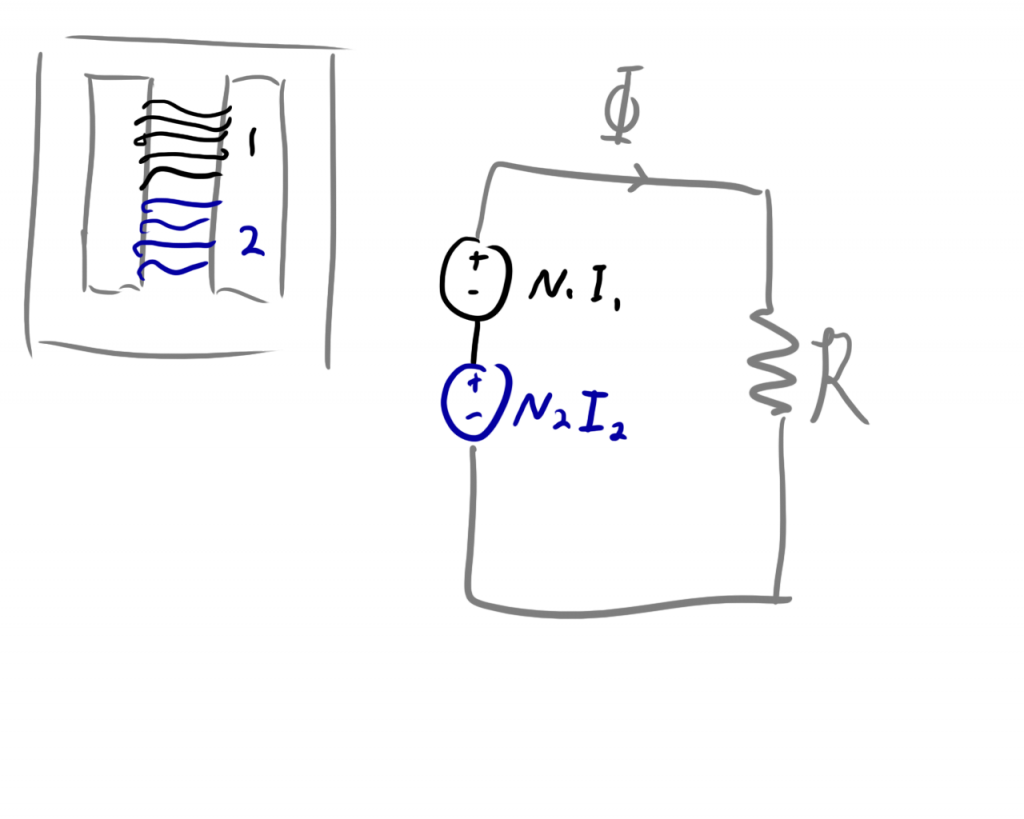 Now as far as the specifics such as what exactly
Now as far as the specifics such as what exactly
![]()
is is irrelevant for this analysis. All you need to know is that these values are equal for both turns of the inductor.
So you’ll note that the MMF contributions of the primary and secondary windings are in series. This is because we’re assuming that all of the flux passing through one also passes through the other. Now let’s test out this model starting with Ohm’s law (but with magnetic fields).
![]()
![]()
Keep in mind that
![]()
is actually the sum of the
![]()
fields produced in each coil.
![]()
![]()
![]()
Alright, so apparently this model holds some water. Now, we’ve said before that in an ideal transformer,
![]()
. That means:
![]()
![]()
There are two possible solutions to this equation. Either
![]()
or
![]()
. The former is an obvious solution. When there is no current in either winding, the magnetic flux is zero, so that’s not very interesting. The latter however is very useful.
![]()
So if you want your transformer to be ideal, you either need to have
![]()
or
![]()
. A zero length is going to be very hard to manufacture as is an infinite area. That leaves
![]()
.
Let’s Talk About Mu
![]()
represents the “magnetic permeability” of a material. Permeability describes the capacity of a space to hold magnetic fields. A vacuum has a permeability (written
![]()
or “mu naught”) which as it turns out is very close to that of air.
As manufacturers try to make better and better transformers, they try to find better and better materials for the core. They record their
![]()
usually as a coefficient of
![]()
sometimes called the “relative permeability” and written as
![]()
. The goal is to have an infinite
![]()
, but they usually top off at about 2000
![]()
for commonly used materials like the ferrite in my core.
Unfortunately,
![]()
is not a constant value inside an inductor. A lot of times, as more and more magnetic field builds up in the core (more current travels around it), the permeability of the material drops. You can see this happening in this graph:
 Which I stole off of this data sheet for powdered metal cores.
Which I stole off of this data sheet for powdered metal cores.
This loss of permeability is called “saturation” and is caused by the reorientation of little magnetic dipoles inside the core material. As a field builds up, dipoles are aligned. When there are no more dipoles left to align, permeability drops. I know this is a very vague explanation, but a thorough understanding is not necessary for this discussion.
Without knowing anything really about my transformer core, I want to hypothesize that my odd voltage ratio (lower than the turns ratio) has something to do with the transformer core saturating. Let’s see if I can demonstrate this trend mathematically.
Not So Perfect After All
So, let’s go back to our flux linkage equation:
![]()
And be a little more explicit about exactly what this means. There will be two flux linkages (one for each winding) and the flux in each winding is partially due the its own current and partially due to the current in the other winding.
![]()
![]()
![]()
If you look at the first term, you’ll see something familiar:
![]()
It looks like the formula for an inductor! We can call this “self-inductance”. It’s the amount that the first winding acts like an inductor as if the second coil wasn’t there. That leaves the second term where the
![]()
is actually
![]()
. We can treat this as an inductor and call it “mutual inductance”. It basically indicates how well linked together the two windings of the transformer are. So, we can rewrite this as:
![]()
Likewise,
![]()
can be written as:
![]()
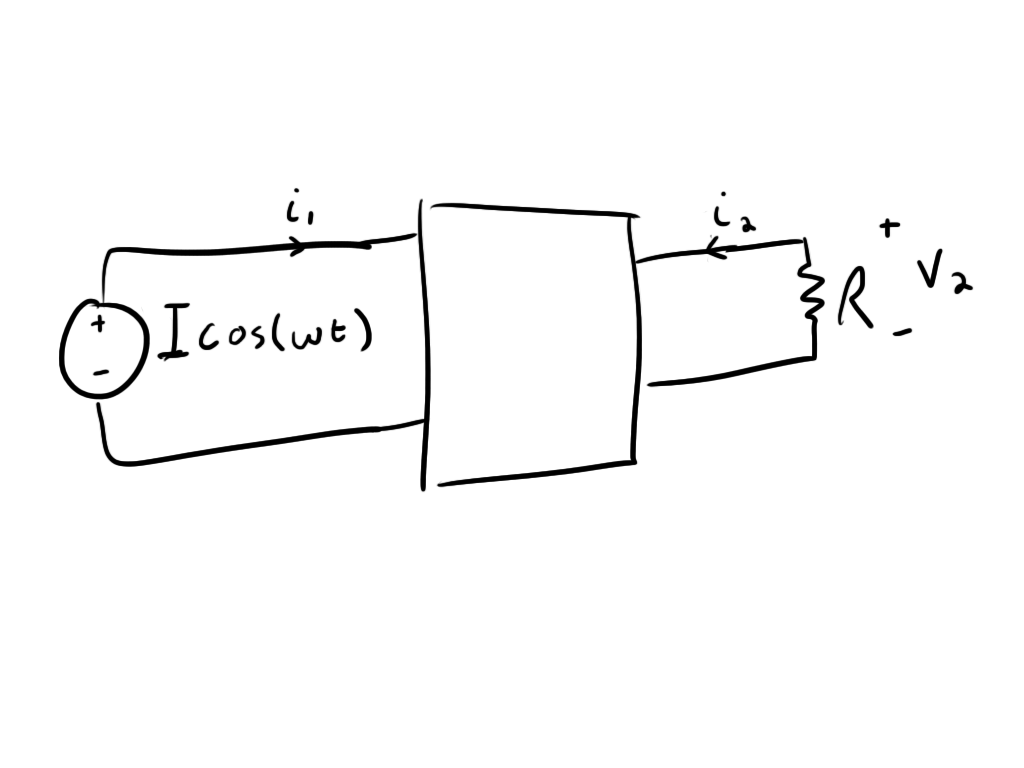
So, to play with our new formulae, let’s set up a fictional scenario where the primary winding is attached to a cosinusoidal current source and the second winding is attached to a resistive load:
![]()
represents the magnitude of the current wave while
![]()
represents the actual current.
So, if we want to see what’s delivered to the load, we need to find the voltage on the secondary winding. We can derive this by taking the time derivative of the flux linkage of the secondary winding:
![]()
![]()
And if we remember from Ohm’s law that
![]()
, we can set our voltage equal to:
![]()
The minus sign is a result of
![]()
being an induced voltage that must be opposite in sign to
![]()
(Lenz’s Law). That’s kind of a weak explanation, but if you’re looking for more solid proof, consider the case where
![]()
is forced to be zero (circuit is opened) and the negative sign isn’t there:
![]()
And you solve for
![]()
![]()
![]()
![]()
![]()
This conclusion means that if there was any current in the secondary winding when you disconnected the primary winding, the current in the secondary would spiral out of control and generate infinite energy dissipation through R. Obviously this is stupid, but if you make the exponent negative, there’s exponential decay, and the current dies down in an orderly fashion.
The sign on
![]()
is less important because it is an isolated system that can be switched around simply by altering the direction of the primary windings.
So, let’s see if we can solve for
![]()
in the more general case. Let’s use the scenario where we are driving our system with a cosinusoidal current source with magnitude
![]()
:
![]()
We’re going to analyze the situation where the system has been running for a very long time and all transient conditions have died off completely. We call this “steady state”, and in steady state, all components are operating at the same frequency. We can thus model the current in the secondary winding as:
![]()
Making the whole system:
![]()
Where
![]()
is the magnitude of the current in the secondary winding. This kind of setup is a perfect situation in which to use phasors. Phasors utilize Euler’s formula:
![]()
where we can replace
![]()
with
![]()
. We can use
![]()
for our analysis as long as we make sure to take the real part of both sides at the end. The idea is that you get all of the exponential terms to cancel out and are left with just relative magnitude and phase information for your system.
(Note, for EEs,
![]()
like it should be)
So we can rewrite our system like this:
![]()
Now, we can start to solve for
![]()
:
![]()
And we can cancel out some terms:
![]()
![]()
Now remember how
![]()
and
![]()
are defined and you can do this:
![]()
![]()
Now we can keep manipulating…
![]()
![]()
![]()
Now, before we bother taking the real part, you can already see some trends. What happens when
![]()
:
![]()
![]()
![]()
So, apparently if
![]()
goes to
![]()
, we get an ideal transformer. So (we’re getting really close here) what do we need to do to approach an ideal transformer? Let’s look at the definition of
![]()
:
![]()
For this quantity to go to
![]()
, we need
![]()
to be infinite! This matches our condition from before. What happens when
![]()
isn’t infinite? The effective turns ratio drops, or:
![]()
So my 1:64 ratio could drop as low as 1:22 and explain the voltage sag I saw at the output.
Imperfect by Design?
I’ve stated before that as current through an inductor rises, the
![]()
of the core drops. Usually, you’d want to have an ideal inductor with infinite
![]()
.
In the case of this cheap power supply, a good non-saturating inductor might have been too big or too expensive, so the designer came up with a better solution. If the core saturates, the input inductance will drop (remember that
![]()
and
![]()
also have
![]()
in them). This is usually a bad thing as the sudden drop in inductance can cause bad current spikes that can cause the transformer to heat up (imagine the transformer suddenly turning into a piece of wire shorted across a power supply).
This is less of a concern here because the transformer is being driven by a resonant circuit so a drastic change in inductance will result in the system just oscillating at a different frequency. What probably happened during design is that the designer realized that the core was going to saturate and rather than trying to use a more expensive/bulkier core, decided to just super saturate the one they had. They could use every last ounce of energy storage it had by adding way more turns than necessary. More copper wire is cheaper than a beefier core.
This also explains why you’re never supposed to run these supplies with out a load. With no current in the secondary winding, you’ll end up fully utilizing that 1:66 turns ratio and get one hell of an output voltage!
Conclusion
- I was measuring a higher inductance than was present due to my ignoring the parasitic capacitance.
- The output voltage drooped because of a saturating transformer core.
- My measurement of the turns ratio through the LC oscillator and input/output voltage measurements was self-consistent entirely by chance.
So if you actually made it this far, I’m amazed. This whole thing just started as a casual review for me and quickly turned into a brief crash course in transformer design. I wrote it mostly as a reference for myself, but if you acquired anything from it, so much the better.
Again, if you find any errors in my work, please let me know! Shoot me an email or leave a comment.
Thanks for reading!


Great article. Tiny nit-pick, it’s “mu naught” not “mu not”.
Tomato tomaughto. Fixed, thanks.
Wouldn’t life have been MUCH easier if you had that 45 alternative. Google for “LC200A” , you can find it for sale lots of places (I bought mine on eBay) and you can find some very positive reviews, including a YouTube side-by-side competition against a huge benchtop LC measuring instrument by Hewlett Packard. If you prefer the joy of building test equipment yourself, there’s quite a sophisticated “Accurate LC meter” kit on sale at electronics-diy.com
45 alternative. Google for “LC200A” , you can find it for sale lots of places (I bought mine on eBay) and you can find some very positive reviews, including a YouTube side-by-side competition against a huge benchtop LC measuring instrument by Hewlett Packard. If you prefer the joy of building test equipment yourself, there’s quite a sophisticated “Accurate LC meter” kit on sale at electronics-diy.com
You’re right that it probably would have been easier, but I also wouldn’t have learned anything. Also, now that I’ve learned from my mistakes, I don’t even need a $45 LCR meter as I can apparently manage with a cap and a scope.
Heh, in honor of your first posts to reddit many days ago, I concidentally found an car audio guy who had a honking huge chinese giant cap. I also estimated the farads with a resistor and a battery. I know not as cool as your scope LC approach, but I did think it was better idea than using the capacitance mode on my multimeter.
Ch00ftech University
Maybe add a reference in transformer design for us lay readers
Thanks
Great article.
oh my gosh… basically for the entire chapter of electromagnetic induction, i thought transformers was the easiest, because i only associated it with the turns ratio, but as it turns out, there is still so much for me to learn! @_@ anyway, great article and thanks so much for the enlightenment! 😀
Pingback: Bringing a Car Battery Back from the Dead: A Ch00ftech Halloween Tale | ch00ftech Industries
dear Sir
would you please say me about the transformer wire characteristics? like A and radios of wires
thx